The Minkowski metric

The equation giving the distance between two points in a particular space is called the metric. Once we know the metric of a space, we know almost everything about the geometry of the space, which is why the metric is of fundamental importance.

We have already met the function that defines the distance between two points in Minkowski spacetime (see Minkowski's Four-Dimensional Space-Time article): it's the spacetime interval given by the formula

ds² = c²Δt² - Δx² - Δy² - Δz²

 This can be written as ds² = 1xc²Δt² - 1xΔx² - 1xΔy² -1xΔz²

And +1, -1, -1, -1 can be defined as the diagonal elements of a 4x4 matrix,  denoted by η_μν: 

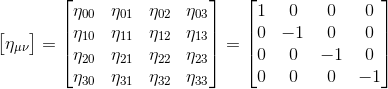
The indices μ,ν after the η symbol identify the elements of the matrix by reference to its rows (μ) and its columns (ν). The convention is that the metric coefficients run from 0 to 3, so η₀₀=1, η₁₁=-1, η₂₂=-1, η₂₁=0, etc.

This matrix simply tells us how to multiply the differentials cdt, dx, dy, dz to obtain the spacetime interval equation. We can see it by writing the matrix product as follow:

So finally, as only η₀₀, η₁₁, η₂₂ and η₃₃ are not null, we get the product equals to

1xc²Δt² - 1xΔx² - 1xΔy² -1xΔz² = c²Δt² - Δx² - Δy² -Δz²

which is the spacetime interval defining Minkoswki spacetime.

Finally, using the index notation, the  Einstein convention (implicit summation on repetead indices) and the Minkowski metric η_μν , we can write the Minkowski line element in a more compact form:

Recall that the symbol η_μν irefers specifically to the Minkowski metric.